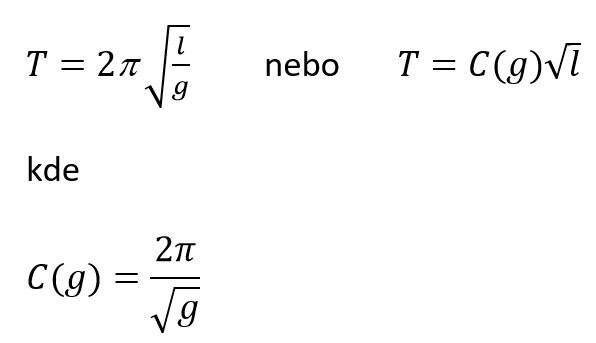1.7rozměr veličiny, rozměr / quantity dimension, dimension of a quantity, dimension
| Termín: | 1.7 rozměr veličiny, rozměr | 1.7 quantity dimension, dimension of a quantity, dimension | ||||||||||||||||||||||||||||||||
| Definice: | vyjádření závislosti veličiny na základních veličinách soustavy veličin jako součinu mocnin činitelů odpovídajících základním veličinám s vynecháním všech číselných činitelů | expression of the dependence of a quantity on the base quantities of a system of quantities as a product of powers of factors corresponding to the base quantities, omitting any numerical factor | ||||||||||||||||||||||||||||||||
| Příklad: | PŘÍKLAD 1 V ISQ je rozměr veličiny síla označen dim F = LMT–2.
PŘÍKLAD 2 V téže soustavě veličin je dim ρB = ML–3 rozměrem veličiny hmotnostní koncentrace složky B a ML–3 je také rozměrem veličiny hustota ρ (objemová hmotnost).
PŘÍKLAD 3 Perioda T kyvadla s délkou l v místě s místním tíhovým zrychlením g je
A tedy dim C(g) = L–1/2 T . | EXAMPLE 1 In the ISQ, the quantity dimension of force is denoted by dim F = LMT–2.
EXAMPLE 2 In the same system of quantities, dim ρB = ML–3 is the quantity dimension of mass concentration of component B, and ML–3 is also the quantity dimension of mass density, ρ (volumic mass).
EXAMPLE 3 The period T of a pendulum of length l at a place with the local acceleration of free fall g is
Hence dim C(g) = L–1/2 T . | ||||||||||||||||||||||||||||||||
| Poznámka 1: | Mocnina činitele je činitel umocněný na exponent. Každý činitel je rozměrem základní veličiny. | A power of a factor is the factor raised to an exponent. Each factor is the dimension of a base quantity. | ||||||||||||||||||||||||||||||||
| Poznámka 2: | Konvenčním symbolickým vyjádřením rozměru základní veličiny je jediné velké písmeno napsané antikvou (stojatým písmem) typu sans-serif (bezpatkové). Konvenčním symbolickým vyjádřením rozměru odvozené veličiny je součin mocnin rozměrů základních veličin v souladu s definicí odvozené veličiny. Rozměr veličiny Q je označován dim Q. | The conventional symbolic representation of the dimension of a base quantity is a single upper case letter in roman (upright) sans-serif type. The conventional symbolic representation of the dimension of a derived quantity is the product of powers of the dimensions of the base quantities according to the definition of the derived quantity. The dimension of a quantity Q is denoted by dim Q. | ||||||||||||||||||||||||||||||||
| Poznámka 3: | Při odvozování rozměru veličiny se neuvažuje, zda veličina má charakter skaláru, vektoru, nebo tenzoru. | In deriving the dimension of a quantity, no account is taken of its scalar, vector, or tensor character. | ||||||||||||||||||||||||||||||||
| Poznámka 4: | V dané soustavě veličin: – veličiny stejného druhu mají stejný rozměr, – veličiny s různými rozměry veličiny jsou vždy různých druhů a – veličiny mající stejný rozměr veličiny nejsou nutně stejného druhu. | In a given system of quantities, - quantities of the same kind have the same quantity dimension, - quantities of different quantity dimensions are always of different kinds, and - quantities having the same quantity dimension are not necessarily of the same kind. | ||||||||||||||||||||||||||||||||
| Poznámka 5: | Značky reprezentující rozměry základních veličin v ISQ jsou:
Tudíž rozměr veličiny Q je označen dim Q = LαMβTγIδΘεNζJη, kde exponenty, nazývané rozměrovými exponenty, jsou kladné, záporné nebo nula. | Symbols representing the dimensions of the base quantities in the ISQ are:
Thus, the dimension of a quantity Q is denoted by dim Q = LαMβTγIδΘεNζJη where the exponents, named dimensional exponents, are positive, negative, or zero. |